Foglie In...Serie Di Fibonacci [Proposta Di Attività Laboratoriale]

Propongo ai colleghi di Scienze un’attività che ho svolto con successo negli anni passati con le mie classi. La condivido qui perché ritengo che sia utile sotto il profilo didattico.

STRATEGIA

Cari ragazzi, lo studio della disposizione delle foglie sul fusto di una pianta vi permette di verificare che, in natura, nulla è lasciato al caso.

Prima di iniziare l’attività, osservate e studiate la fig. 1 e le indicazioni ivi riportate a proposito di un rametto di ciliegio.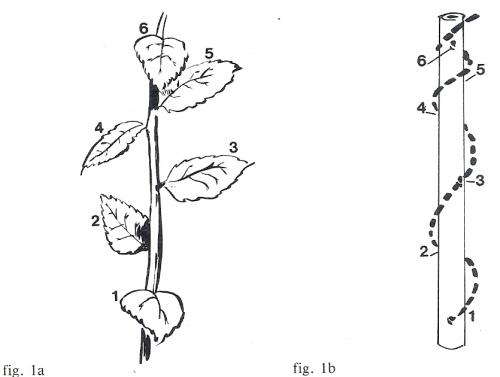

Il rametto è raffigurato nella figura 1 a. La prima foglia del rametto è situata sotto la corrispondente foglia 6. Le altre foglie sono disposte in vari punti attorno al rametto. E’ come se stessero su una spirale (fig. 1b).

La spirale incomincia dalla foglia 1, poi incontra la foglia 2, poi la 3, la 4, la 5 e, alla fine del secondo giro, incontra la foglia 6, che, come detto in precedenza, si trova nella stessa direzione della foglia 1.

In definitiva, ci vogliono due giri per ritrovare due foglie che stiano l’una sopra l’altra e il numero di foglie che le separa è 5.

Per il ciliegio:

numero di giri = 2

numero di foglie = 5

In altre piante (quercia, faggio, noce, ecc.) si verificano altre possibilità: ad esempio bisogna fare non più di 2 giri per trovare foglie che stiano esattamente l’una sopra l’altra, ma 3 oppure 8 giri; così pure varierà il numero delle foglie che si trovano tra le due foglie menzionate.

Le diverse possibili disposizioni delle foglie le potete scoprire voi stessi se seguite le indicazioni riportate nell’ attività qui illustrata.

MATERIALI

Alcuni rami di piante con foglie; se non è necessario, non spezzate i rami: potete fare sul posto le vostre osservazioni.

ATTIVITA’

1.       Una volta scelta la pianta ed il suo ramo, segnatevi a mente una foglia. Partite da quella foglia e guardate dove è posta un’altra foglia che stia nella stessa posizione della prima.

2.       Contate il numero delle foglie che stanno intorno al ramo nel tratto che separa la foglia da cui siete partiti da quella che sta nella sua stessa posizione, come nel caso del rametto del ciliegio (fig. 2).

 

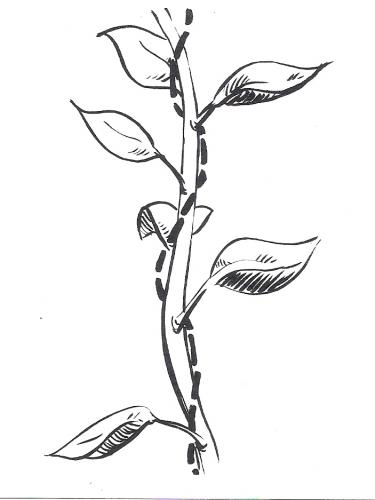
Figura 2

3.    Proseguite in questo modo: contate i giri che occorre effettuare intorno al ramo per andare dalla prima foglia all’altra che si trova nella stessa posizione e il numero di foglie che le separano.

 Riportate i dati rilevati:

numero dei giri = …

numero delle foglie = ...

4. Scegliete un’altra pianta (faggio, noce) e ripetete dal punto 1 al punto 3.

5. Provate con parecchie piante. Anzi, provateci tutte le volte che avete l’occasione di trovarvi di fronte ad una pianta ( e se non siete impegnatissimi…con altri giochi)

RIFLETTIAMO

1. La posizione delle foglie sul fusto è caratteristica e costante per ogni specie vegetale. Il suo studio è detto fillotassi (dal greco: phyllon = foglia e taxis= ordine.).

2.  Leonardo da Vinci (1452-1519) si accorse della regolarità della posizione delle foglie sul fusto e così espresse nel suo scritto Trattato della pittura (libro sesto) in un italiano di 400 anni fa: “ Ha posto la natura delle foglie degli ultimi rami di molte piante, ché sempre la sesta foglia è sopra la prima e così prosegue successivamente se la regola non è impedita”. Anche per Leonardo era chiaro che la regola sulla posizione delle foglie non è rispettata se non ci sono le condizioni per il suo verificarsi.

3. Per quale motivo le foglie si distribuiscono in un certo ordine…e non a caso? Come sapete in natura ogni fenomeno ha una sua spiegazione: questa volta la spiegazione si trova nella vita delle piante e nel suo svilupparsi. Esprimete una vostra ipotesi sulla disposizione delle foglie e discutetela con il vostro insegnante. Riassumete brevemente i risultati della vostra indagine nel quaderno di laboratorio.

ALTRE POSSIBILITA’

A) Nel caso del ciliegio, il numero di giri trovato è stato 2 mentre il numero di foglie era 5. I due numeri 2 e 5 li ritrovate nella tabella A qui riportata:

Tabella A – Esempio di serie di Fibonacci

Numero di giri       1         1            2           3            5              8

Numero di foglie   2         3            5           8           13            21

  

In altre piante si sono trovati altri numeri: in 1 giro si trovano 3 foglie; oppure in 3 giri 8 foglie, ecc. Tali numeri si ritrovano anche nella Tabella A, testimoniando una regolarità numerica nella disposizione delle foglie sul fusto.

 Anche a voi è capitato, nelle vostre osservazioni e conteggi di foglie, di verificare qualche valore indicato nella Tabella A?

 B)      Che cosa ha di particolare la Tabella A? Osservate il numero 5: esso è ottenuto dalla somma dei due numeri che lo precedono, cioè  2 + 3, mentre il numero 8 è dato da 5 + 3; così altri numeri sono ottenuti dalla somma dei due che li precedono. La serie di numeri che si ottiene è chiamata: serie di Fibonacci, dal nome del suo scopritore vissuto quasi 800 anni fa tra il 1180 e il 1250.

C)      La successione di numeri della tabella A è uno degli esempi di successione. Infatti si possono considerare altre sequenze. Ad esempio:

Numero dei giri =                1          2          3          5          8

Numero delle foglie =         2          3           5         8          13

Dicono che nel faggio e nel noce valgono i numeri 2 (numero dei giri) e 3 (numero delle foglie); mentre per la quercia e l’albicocco valgono i numeri 5 (giri) e 8 (foglie). Se ne avete occasione, verificate questi dati numerici.

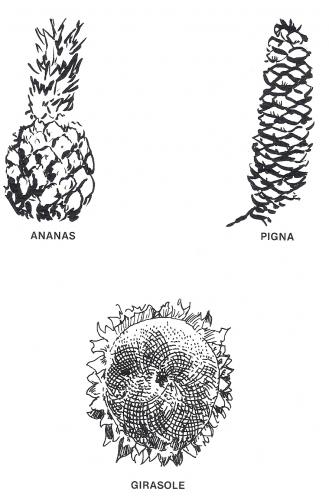
D)     Non solo le foglie sono costruite in… serie. Le protuberanze sulla scorza di un ananas sono distribuite in spirali, alcune in senso orario ed altre in senso antiorario: il rapporto è di 8 a 13 ( 8 in una direzione e 13 nell’altra). In una pigna il rapporto tra le spirali è di 5 a 8. Le spirali formate dai semi del girasole sono in rapporto di 34 a 55.

Controllate questi numeri che rientrano tutti in una serie costruita in modo tale che ogni numero è la somma dei due che lo precedono:

1        2         3        5       8       13       21       34       55…

 Potete scaricare il post in formato di file pdf, per utilizzarlo come scheda di lavoro.

Consultate la sezione "Materiali Didattici" su questo blog.