Se volete saperne di più andate sul blog "Splash ragazzi" della maestra Renata e della sua classe 3° A.
Nella foto seguente, si riescono a intravedere le quattro uova, deposte in questo mese di marzo.
domenica 30 marzo 2008
Aria E Vento: Una Coppia Speciale Di Falchi Pellegrini
Aria e Vento sono una coppia di falchi pellegrini, che hanno nidificato sull'edificio della Facoltà di Economia dell'Università della Spienza di Roma.
Se volete saperne di più andate sul blog "Splash ragazzi" della maestra Renata e della sua classe 3° A.
Nella foto seguente, si riescono a intravedere le quattro uova, deposte in questo mese di marzo.
Se volete saperne di più andate sul blog "Splash ragazzi" della maestra Renata e della sua classe 3° A.
Nella foto seguente, si riescono a intravedere le quattro uova, deposte in questo mese di marzo.
Observatory: La Soluzione
Cari ragazzi, amici e lettori,
vi ringrazio della partecipazione e vi rivolgo le mie congratulazioni.
Le vostre soluzioni sono state sostanzialmente tre:
1. 700 giorni
2. 140 giorni
3. 70 giorni.
Per quanto riguarda la prima, l'argomentazione basata sul calcolo aritmetico del m.c.m. di 100 e 350 non è errata, ma parziale come vedremo. I miei complimenti, comunque, a Enzo e Arianna che, avendo soltanto 11 anni, ha sfruttato gli strumenti matematici di cui è in possesso.
La seconda soluzione è esatta, se si considera soltanto l'allineamento pianeta - pianeta - sole.
La terza soluzione, infine, è quella esatta, tenuto conto, come osservato da Lillyth che c'è allineamento anche quando si ha la configurazione: pianeta - sole - pianeta.
Riporto, pertanto, l'argomentazione di Lillyth.
I pianeti, infatti, sono allineati al sole anche quando questo è in mezzo a loro e si trovano tutti e tre i corpi celesti su di un'unica retta. In questo caso basta calcolare quando gli archi di orbita tracciati hanno 180° di differenza, cioè dopo 70 giorni infatti: (360°:100x70)-(360°:350x70)=180°
Mikelo, sulla base dei ragionementi di Lubbra e di Lillyth, è andato alla ricerca di una formula risolutiva:
1= angolo giro
1/100 di giro al giorno per un pianeta, 1/350 di giro per l'altro.
x (1/100 - 1/350) =1/2
x [(7-2)/700] = 1/2
x (5/700) =1/2
x= 1/2 * 700/5 = 700/10 = 70
Ricapitolando, la domanda, come avete giustamente osservato, poteva dare adito a qualche dubbio. Però, poiché si richiede quando i due pianeti saranno nuovamente allineati, occorre tenere conto dei due diversi tipi di allineamento.
Pertanto, la soluzione esatta è 70 giorni.
Grazie ancora a tutti voi per aver partecipato...e rimanete sintonizzati per altri puzzle!
__________________________________
vi ringrazio della partecipazione e vi rivolgo le mie congratulazioni.
Le vostre soluzioni sono state sostanzialmente tre:
1. 700 giorni
2. 140 giorni
3. 70 giorni.
Per quanto riguarda la prima, l'argomentazione basata sul calcolo aritmetico del m.c.m. di 100 e 350 non è errata, ma parziale come vedremo. I miei complimenti, comunque, a Enzo e Arianna che, avendo soltanto 11 anni, ha sfruttato gli strumenti matematici di cui è in possesso.
La seconda soluzione è esatta, se si considera soltanto l'allineamento pianeta - pianeta - sole.
La terza soluzione, infine, è quella esatta, tenuto conto, come osservato da Lillyth che c'è allineamento anche quando si ha la configurazione: pianeta - sole - pianeta.
Riporto, pertanto, l'argomentazione di Lillyth.
I pianeti, infatti, sono allineati al sole anche quando questo è in mezzo a loro e si trovano tutti e tre i corpi celesti su di un'unica retta. In questo caso basta calcolare quando gli archi di orbita tracciati hanno 180° di differenza, cioè dopo 70 giorni infatti: (360°:100x70)-(360°:350x70)=180°
Mikelo, sulla base dei ragionementi di Lubbra e di Lillyth, è andato alla ricerca di una formula risolutiva:
1= angolo giro
1/100 di giro al giorno per un pianeta, 1/350 di giro per l'altro.
x (1/100 - 1/350) =1/2
x [(7-2)/700] = 1/2
x (5/700) =1/2
x= 1/2 * 700/5 = 700/10 = 70
Ricapitolando, la domanda, come avete giustamente osservato, poteva dare adito a qualche dubbio. Però, poiché si richiede quando i due pianeti saranno nuovamente allineati, occorre tenere conto dei due diversi tipi di allineamento.
Pertanto, la soluzione esatta è 70 giorni.
Grazie ancora a tutti voi per aver partecipato...e rimanete sintonizzati per altri puzzle!
__________________________________
POST CORRELATO
sabato 29 marzo 2008
Catene E Reti Alimentari [Learning Object]
Cari ragazzi di 1° A,
ormai ci siamo addentrati nello studio dell'ambiente e abbiamo appena trattato le catene e le reti alimentari. E' giunto, quindi, il momento di presentarvi un Learning Object inerente tale tematica.
Un Learning Object (LO) è un oggetto di apprendimento multimediale, dinamico e interattivo, come constaterete, che può rappresentare un modo interessante e divertente per consolidare o potenziare quanto avete già studiato.
Quelle che seguono sono alcune schermate del LO.
Segue la schermata relativa ad una simulazione in flash, che è possibile rivedere più volte.
Ci sono verifiche interattive che non vi permetteranno di proseguire se prima non avrete risposto correttamente.
C'è anche la possibilità di consultare pagine tutoriali e/o di approfondimento come la seguente.
E non è finita! Potrete consultare, inoltre, pagine di glossario e tutoriali e altro che scoprirete.
Il Learning Object è stato prodotto da Garamond ( che ringrazio per la concessione) nell'ambito del progetto ministeriale "Apprendere Digitale". La sottoscritta ne ha redatto il progetto didattico generale e i testi.
Grandi e piccini, se volete saperne di più sui Learning Object e sul Progetto apprendere digitale, vi rimando a questi due articoli da me pubblicati sulla rivista Scuola e Didattica, Editrice La Scuola.
>> Scarica il Learning Object
Il file zippato che scaricherete, deve essere decompresso. Successivamente, lanciate il file html "start". Non c'è bisogno di installare niente perchè il LO è autoconsistente.
Se volete consultare i credits, cliccate sul bottone i, presente sulla barra laterale del LO.
____________________________
POST CORRELATI
martedì 25 marzo 2008
Meccanica Quantistica: L'esperimento Delle Due Fenditure In Un Video
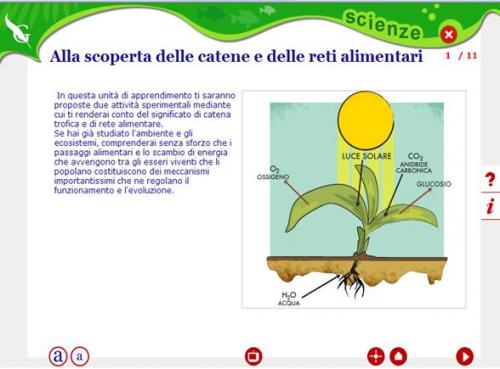
Cari ragazzi, il video che vedete in questo post riguarda un famoso esperimento di Meccanica Quantistica, l'esperimento delle due fenditure
Su Wikipedia, leggiamo in proposito:
"La Meccanica Quantistica, o fisica quantistica, è un ramo della fisica con numerose applicazioni sia sperimentali che teoriche. Gli effetti della meccanica quantistica a livelli macroscopici non sono generalmente apprezzabili, in quanto diventano evidenti solo per scale atomiche o subatomiche; inoltre, essa fornisce una generalizzazione di tutte le teorie classiche, esclusa la teoria della relatività, e dà un'accurata descrizione di molti fenomeni precedentemente inspiegabili come la radiazione di corpo nero e la stabilità degli atomi introducendo il concetto di orbitali degli elettroni.
«Più la teoria dei quanti ha successo, più sembra una sciocchezza»
(Albert Einstein, lettera a Heinrich Zangger, 20 maggio 1912)
La meccanica quantistica riunisce un complesso di teorie fisiche formulate nella prima metà del ventesimo secolo che descrivono il comportamento della materia a livello microscopico, a scale di lunghezza inferiori o dell'ordine di quelle dell'atomo o ad energie nella scala delle interazioni interatomiche, dove cadono le ipotesi alla base della meccanica classica. Essa permette di interpretare e quantificare fenomeni che, nell'opinione della maggior parte dei fisici contemporanei, non possono essere giustificati dalla meccanica classica, le cui previsioni sono in questi casi in completo disaccordo con i risultati sperimentali".
Questo argomento è troppo complesso per voi, ma ho voluto presentare il video per i nostri lettori adulti perché illustra in maniera chiara i fondamenti della meccanica quantistica. L'esperienza filmata è, come detto prima, quella celebre delle due fenditure, nella quale secondo il fisico Feynman, si può osservare la stranezza del comportamento quantistico.
[ Via| Il Potere Della Fantasia ]
Primavera: Un Campo Di Fiori Violetti In Arkansas
Cari ragazzi, da qualche giorno siamo in primavera anche se non si direbbe, date le giornate per nulla primaverili.
Allora ho pensato di attingere alle risorse fotografiche della brava Gale Rainwater per risollevarci un po' lo spirito. Guardate la foto che ho scelto. E' di una bellezza straordinaria: un campo di fiori violetti in Arkansas!
Avete notato che c'è un unico albero? Curioso vero? Sembrerebbe quasi il guardiano di tanta bellezza!
__________________________________________
Allora ho pensato di attingere alle risorse fotografiche della brava Gale Rainwater per risollevarci un po' lo spirito. Guardate la foto che ho scelto. E' di una bellezza straordinaria: un campo di fiori violetti in Arkansas!
Avete notato che c'è un unico albero? Curioso vero? Sembrerebbe quasi il guardiano di tanta bellezza!
__________________________________________
POST CORRELATI
- Riflesso In Autunno: Maroon Belles (Colorado)
domenica 23 marzo 2008
Observatory: Risolvi Il Puzzle Astronomico
Ed ecco qui, cari ragazzi e lettori, la proposta di risolvere un puzzle, a mio avviso interessante e divertente.
Osservate con attenzione l'immagine seguente.
Il puzzle propone quanto segue.
In un sistema solare lontano, molto lontano, due pianeti sono perfettamente in linea con il loro sole (come nell'immagine).
Icerix, il pianeta più freddo e più lontano, impiega 350 giorni per descrivere un'orbita completa attorno al sole.
Cetacearth, il pianeta pieno d'acqua più, vicino al sole, impiega soltanto 100 giorni.
Ipotizzando che le orbite siano nello stesso piano, in quanti giorni i due pianeti saranno di nuovo allineati con il loro sole?
Per la soluzione, non occorrono concetti complessi di geometria angolare/rotazionale.
Per voi ragazzi, la risoluzione sarà possibile più in là quando avrete acquisito i necessari pre-requisiti strumentali, ma nulla vieta che ci proviate.
Sarebbe alquanto gradito il cimento dei lettori, appassionati di queste tematiche.
I colleghi coglieranno sicuramente la validità didattica della proposta.
__________________________________
POST CORRELATI
Osservate con attenzione l'immagine seguente.
Il puzzle propone quanto segue.
In un sistema solare lontano, molto lontano, due pianeti sono perfettamente in linea con il loro sole (come nell'immagine).
Icerix, il pianeta più freddo e più lontano, impiega 350 giorni per descrivere un'orbita completa attorno al sole.
Cetacearth, il pianeta pieno d'acqua più, vicino al sole, impiega soltanto 100 giorni.
Ipotizzando che le orbite siano nello stesso piano, in quanti giorni i due pianeti saranno di nuovo allineati con il loro sole?
Per la soluzione, non occorrono concetti complessi di geometria angolare/rotazionale.
Per voi ragazzi, la risoluzione sarà possibile più in là quando avrete acquisito i necessari pre-requisiti strumentali, ma nulla vieta che ci proviate.
Sarebbe alquanto gradito il cimento dei lettori, appassionati di queste tematiche.
I colleghi coglieranno sicuramente la validità didattica della proposta.
__________________________________
POST CORRELATI
- La Nebulosa Rosetta Per Il Valentine's Day
- L'Universo Visto Da Un'Astronave
- Conspiracy Of Science - Earth Is In Fact Growing
- L'Universo Visto Da Un'Astronave
- Conspiracy Of Science - Earth Is In Fact Growing
Buona Pasqua Con Gioco E Segnalazioni Scientifiche
Cari ragazzi, come vi avevo promesso ecco un gioco per i momenti di relax di queste giornate di vacanza, ma anche per gli altri giorni.
Naturalmente, il gioco è messo a disposizione anche di amici e lettori del blog.
Dopo il gioco, qualche informazione scientifica interessante.
Scoperto il più grande buco nero dell'Universo. Questa massa farebbe invidia ad una intera Galassia! 18 miliardi di Soli è una massa davvero straordinaria per questo buco nero, il più pesante che sia mai stato trovato. Si trova a 3,5 miliardi di anni luce in un quasar chiamato OJ287.
_____________________________________
POST CORRELATI
- La Nebulosa Rosetta Per Il Valentine's Day
- L'Universo Visto Da Un'Astronave
- Conspiracy Of Science - Earth Is In Fact Growing
Naturalmente, il gioco è messo a disposizione anche di amici e lettori del blog.
E' un gioco carino, in cui devi far scoppiare le bolle prima che queste facciano scoppiare te! [Il gioco non è più attivo. Lo sostituirò con un altro funzionante].
Dopo il gioco, qualche informazione scientifica interessante.
Scoperto il più grande buco nero dell'Universo. Questa massa farebbe invidia ad una intera Galassia! 18 miliardi di Soli è una massa davvero straordinaria per questo buco nero, il più pesante che sia mai stato trovato. Si trova a 3,5 miliardi di anni luce in un quasar chiamato OJ287. A 7, 5 MLD DI ANNI LUCE LA PIU'GRANDE ESPLOSIONE COSMICA
Mercoledì notte nel cielo dell'emisfero nord per un'ora la sfera celeste è stata illuminata dalla più grande esplosione mai registrata di una stella. Malgrado la deflagrazione cosmica sia avvenuta a 7,5 miliardi di anni luce da noi, essa è stata così potente che si poteva vedere a occhio nudo, in direzione della costellazione dell'Orsa minore. Prima di esplodere, spiegano alla Nasa, la stella era una gigante rossa, 40 volte più grande del nostro sole. (AGI) - Washington, 21 mar.
E' tutto! Auguro calorosamente, a voi cari ragazzi e ai nostri lettori,
_____________________________________
POST CORRELATI
- La Nebulosa Rosetta Per Il Valentine's Day
- L'Universo Visto Da Un'Astronave
- Conspiracy Of Science - Earth Is In Fact Growing
venerdì 21 marzo 2008
Il Magnetismo: Il Seguito Dell'attività Della Classe 3° A PrimariaDi "Splash Ragazzi"
Cari ragazzi di 1° e 2°, come ricorderete, tempo fa pubblicai un articolo dal titolo "Il Magnetismo: Le Domande Difficili Di Una Classe 3° Primaria", dedicato agli alunni della classe 3° A primaria di Splash ragazzi.
Ebbene l'attività ha avuto un seguito. Gli alunni della quinta A (una classe della stessa scuola della 3° A) con la maestra Anita (una collega della maestra Renata) hanno tenuto una lezione ai loro compagni più giovani.
Ne è scaturito un percorso bello e significativo.
La maestra Renata ha anche realizzato una serie di diapositive del mio articolo, contenente le risposte da me fornite alle domande dei suoi alunni.
Potete vedere direttamente di seguito le diapositive o scaricarle seguendo il link segnalato alla fine del post.
Cari bambini di Splash Ragazzi, ho preparato per voi un test sul magnetismo che potete scaricare, stampare e compilare, se vi fa piacere.
domenica 16 marzo 2008
I Geni Architetti Del Cervello: Una Interessante Ricerca
Cari ragazzi, amici e lettori,
ricordate gli interessanti contributi del nostro amico Gaetano sulla questione dell'intelligenza matematica, che tanto successo hanno riscosso tra voi?
Ebbene, l'articolo che segue, sempre dello stesso autore (che ringrazio per l'ennesima volta), percorre quella stessa via. Vi invito quindi a leggerlo con attenzione perché merita veramente!
...ragazzi aspetto i vostri commenti, come al solito!
Nel blog Matem@ticaMente (consulta i link alla fine di questo articolo) si è acceso non molto tempo fa un coinvolgente convivio scaturito da argomenti che ho tratto dal libro “Intelligenza matematica” di Brian Butterworth. Indubbiamente, il merito va al tema dell'argomento trattato e questo incoraggia a continuare su questa strada per il produttivo approccio, specie con i giovani cui è dedicato questo blog.
"Tutto ha inizio – afferma questo insigne scienziato – dalla consapevolezza che ogni essere umano nasce col senso dei numeri grazie al cosiddetto gene della matematica". E poi rileva che l'abilità matematica nei bambini dipende dal normale sviluppo dei “moduli numerici”, posseduti alla nascita. Di qui, tutta una serie di chiarimenti prodotti dal prof. Butterworth che sono stati riepilogati nel post del suddetto blog Matem@ticaMente.
Del gene della matematica se ne è occupato compiutamente un altro luminare, il prof. Devlin Keith docente di Matematica al Saint Mary's College di Stanford – California, autore appunto del libro “Il gene della matematica”. E qui sorge l'interesse scientifico per capire, per esempio, che cosa differenzia un matematico da una persona che si considera assolutamente incapace di sviluppare una qualsiasi argomentazione matematica? Attitudine? Predisposizione? O addirittura genetica?
Si osserva che senso del numero e ragionamento matematico, spesso confusi, appartengono a piani sostanzialmente differenti. Il primo è comune a vari animali (oltre all’uomo): numerosi esperimenti mostrano che scimpanzé, ratti, leoni e colombi, per esempio, posseggono la capacità di confrontare il numero di oggetti di insiemi diversi; il che comporta un evidente vantaggio ai fini della sopravvivenza.
La possibilità di argomentare matematicamente è invece una prerogativa esclusivamente umana e, a parere di Devlin Keith, essa ha origine dalla stessa facoltà cerebrale che ci consente di usare il linguaggio, ossia la capacità simbolica.
La conquista dell’astrazione, fondamentale per comprendere il mondo, organizzarsi e dunque per la stessa sopravvivenza dell’uomo sulla Terra, fu il passaggio cruciale che permise al discendente di Homo erectus di sviluppare sia il linguaggio sia il ragionamento matematico. Pertanto, non solo il gene della matematica non esiste (il titolo ha valore chiaramente provocatorio!), ma la Matematica ci appartiene; è una delle nostre usuali facoltà mentali così come lo è la capacità di esprimerci attraverso il linguaggio. [1]
Se queste argomentazioni ci giungono da parte di ricercatori tutti occupati dal risvolto strettamente connesso alla scienza matematica, è interessante completare, in questa sede didattica scolare di scienze, anche il risvolto che riguarda la ricerca della scienza biogenetica, poiché è stato continuamente tirato in ballo il gene della matematica fra i diversi altri geni.
È interessante il percorso della ricerca scientifica biogenetica – la biologia molecolare in particolare – seguito da un noto ricercato, il prof. Edoardo Boncinelli. Tempo addietro, nel 1998 ha espresso, com'è suo solito in modo davvero pittoresco, le sue concezioni in biogenetica riportate dalla rivista mensile Newton di ottobre. Sintetizzo di seguito l'articolo a riguardo pubblicato su questo periodico.
Secondo Boncinelli, la testa dell’uomo, come di qualsiasi vivente, nel cominciare a prefigurarsi alla vita terrena, segue un certo itinerario genetico, in netto anticipo sul resto, pur esso in formazione secondo gli schemi cromosomici.
«I geni che formano la testa cominciano a funzionare quando ancora l’embrione “non sa” dove avrà la testa e dove i piedi. In questa fase, la porzione dell‘embrione che diventerà la testa è smisuratamente grande rispetto al resto, come se la natura si sia voluta concentrare sulla parte più nobile di un individuo, lasciando perdere temporaneamente il resto».
I suddetti geni architetti – prosegue il prof. Boncinelli – «probabilmente rappresentano la nostra parte più antica rimasta sostanzialmente inalterata da quando comparvero sulla terra i primi animali dotati di testa, cioè subito dopo le meduse nella scala evolutiva». Di qui si rivela il lato giocoso e polarizzante di Boncinelli con una conclusione a modo suo congeniale. Egli dice che «la bellezza di questa ricerca è proprio nell‘aver mostrato che il progetto fondamentale del corpo umano è stato deciso centinaia di milioni di anni fa e che tutti gli animali oggi esistenti, uomo compreso, non rappresentano che delle variazioni al tema».
«Un bambino inizia a svilupparsi con l’attivazione di questi geni “preistorici”, quindi, è come se in pochi giorni ripercorresse l’intera storia evolutiva».
In particolare, Boncinelli ed il suo gruppo di ricercatori del Dipartimento di biotecnologie dell’Istituto San Raffaele di Milano, avevano fatto progredire le ricerche sui geni architetti del cervello, scoprendone un altro, chiamato EMX-2.
Il ruolo di EMX-2 nella progettazione e costruzione della corteccia cerebrale venne chiarito dallo stesso gruppo nel 2000 e allora si parlò di EMX-2 come del “gene che regola il pensiero”. Anche adesso l’entusiasmo è grande.
Per Michèle Studer, il processo di suddivisione cerebrale controllato dal gene COUP-TFI potrebbe costituire la base neurologica della famosa “teoria delle intelligenze multiple”, elaborata 25 anni fa da Howard Gardner, professore di psicologia dell’età evolutiva all’Università di Harvard, a partire da osservazioni sullo sviluppo delle capacità cognitive nei bambini. La teoria di Gardner scardinò il tradizionale concetto di intelligenza, intesa come capacità generale, misurabile con il QI, sostenendo che l’intelligenza risulta dalla combinazione di alcune abilità mentali più o meno sviluppate, o meglio, esistono diversi tipi di intelligenza, sette o anche otto o forse più. In realtà la teoria psicologica di Gardner ha rivoluzionato anche il modo di vedere il sistema cervello-mente: non un elaboratore centrale, ma l’insieme di sistemi di elaborazione fondamentali e distinti. La ricerca dei geni - probabilmente più di due, forse una decina - responsabili di questa straordinaria architettura è aperta.
Per chi volesse approfondire la cognizione sulla ricerca del prof. Boncinelli, rimando ad un pdf presente sul sito dell'università di Udine (consulta il link alla fine del post).
Geni architetti “dilettanti”- L'opinione di un dilettante
Nello studio della matematica, c’è opinione degli stessi accademici che, per prima cosa, molte creazioni matematiche sono storicamente state fatte da cosiddetti “dilettanti” (che è poi solo un modo di dire: a volte la loro cultura è tutt’oggi invidiabile da parte di tanti “accademici”). Per seconda cosa, quel che conta nella ricerca matematica è spesso lo spirito creativo, l’idea geniale, la curiosità, doti che non sempre richiedono una grande cultura matematica.
Ma le creazioni riguardano anche innumerevoli altre discipline della scienza e perciò anche in tutti questi ambiti si annoverano altrettante creazioni attribuite ai “dilettanti” in questione.
Ne abbiamo una prova proprio nel contesto di questo scritto, con il prof. Boncinelli, fisico di formazione, ma biologo molecolare di mestiere, oggi anche filosofo.
Chi abbiamo di fronte? Per certi versi, senza per questo sminuire il suo indubbio prestigio accademico, potremo accettare l'idea che la sua carriera di ricercatore insigne è cominciata in modo “dilettantististico” partendo, però, da una posizione di tutto riguardo, la laurea in fisica.
Boncinelli ha dunque cominciato a “nascere” come studioso “autodidatta” delle scienze della vita, ed è diventato poi pioniere delle discipline scientifiche che attualmente hanno raggiunto i massimi livelli di specializzazione. Discipline che alla fine degli anni ’60 cominciavano a muovere i loro primi passi.
Ma, per certi altri versi, è così anche per il prof. Butterwort, professore di neuropsicologia cognitiva, col suo libro “Intelligenza matematica”, per esempio. Ha affrontato un considerevole lavoro addentrandosi nel mondo dei numeri, eppure egli sin dall'inizio della stesura del suddetto libro ci tiene a dire: «Io non sono un matematico. In effetti, non sono particolarmente bravo né in matematica né a far calcoli.»
Un altro esempio, che sembra avere le connotazioni risalenti a geni del genere “dilettante”, è il caso di Hunting del film «Will Hunting, genio ribelle», del quale ne parlo nel post «Competenti e incompetenti con i numeri» di Matem@ticaMente.
Egli è un giovanotto che lavora come inserviente al MIT, la più prestigiosa Università scientifìca del mondo. Si tratta però di un film, ma la sua trama è interessantissima, non solo sotto il profilo umano, ma anche per il lato scientifico che con questo scritto si sta affrontanto, senza alcuna pretesa accademica naturalmente. È una mia semplice opinione di meno che dilettante in materia.
E così, seguendo la trama del film in discussione, si viene scoprire che Will Hunting risulta essere un prodigio in matematica alla stregua di Ramanuhjan, il più grande di tutti.
Il professore che poi si occupa con amore di lui, pur essendo insignito di una medaglia Fields – una specie di premio Nobel per la matematica, solo che viene assegnata ogni quattro anni – ne è affascinato. «Non sono niente in confronto a questo ragazzo», ammette.
Gaetano Barbella
- Scarica il pdf sulla ricerca del prof. Boncinelli: "L'origine della forma vivente"
_________________________________
POST CORRELATI
- Intelligenza Matematica
- Tabelline e Matematica
- Competenti E Incompetenti Con I Numeri
ricordate gli interessanti contributi del nostro amico Gaetano sulla questione dell'intelligenza matematica, che tanto successo hanno riscosso tra voi?
Ebbene, l'articolo che segue, sempre dello stesso autore (che ringrazio per l'ennesima volta), percorre quella stessa via. Vi invito quindi a leggerlo con attenzione perché merita veramente!
...ragazzi aspetto i vostri commenti, come al solito!
__________________
PREMESSA
Nel blog Matem@ticaMente (consulta i link alla fine di questo articolo) si è acceso non molto tempo fa un coinvolgente convivio scaturito da argomenti che ho tratto dal libro “Intelligenza matematica” di Brian Butterworth. Indubbiamente, il merito va al tema dell'argomento trattato e questo incoraggia a continuare su questa strada per il produttivo approccio, specie con i giovani cui è dedicato questo blog.
Mi è sorta così l'idea di ampliare l'argomento emergente dal suddetto libro sotto il profilo della scienza, onde ravvisarvi la reale possibilità. Parto perciò da alcune cose sostanziali esposte nel blog Matem@ticaMente per bocca di Brian Butterworth, l'autore del testo in questione.
"Tutto ha inizio – afferma questo insigne scienziato – dalla consapevolezza che ogni essere umano nasce col senso dei numeri grazie al cosiddetto gene della matematica". E poi rileva che l'abilità matematica nei bambini dipende dal normale sviluppo dei “moduli numerici”, posseduti alla nascita. Di qui, tutta una serie di chiarimenti prodotti dal prof. Butterworth che sono stati riepilogati nel post del suddetto blog Matem@ticaMente.
Del gene della matematica se ne è occupato compiutamente un altro luminare, il prof. Devlin Keith docente di Matematica al Saint Mary's College di Stanford – California, autore appunto del libro “Il gene della matematica”. E qui sorge l'interesse scientifico per capire, per esempio, che cosa differenzia un matematico da una persona che si considera assolutamente incapace di sviluppare una qualsiasi argomentazione matematica? Attitudine? Predisposizione? O addirittura genetica?
Si osserva che senso del numero e ragionamento matematico, spesso confusi, appartengono a piani sostanzialmente differenti. Il primo è comune a vari animali (oltre all’uomo): numerosi esperimenti mostrano che scimpanzé, ratti, leoni e colombi, per esempio, posseggono la capacità di confrontare il numero di oggetti di insiemi diversi; il che comporta un evidente vantaggio ai fini della sopravvivenza.
La possibilità di argomentare matematicamente è invece una prerogativa esclusivamente umana e, a parere di Devlin Keith, essa ha origine dalla stessa facoltà cerebrale che ci consente di usare il linguaggio, ossia la capacità simbolica.
La conquista dell’astrazione, fondamentale per comprendere il mondo, organizzarsi e dunque per la stessa sopravvivenza dell’uomo sulla Terra, fu il passaggio cruciale che permise al discendente di Homo erectus di sviluppare sia il linguaggio sia il ragionamento matematico. Pertanto, non solo il gene della matematica non esiste (il titolo ha valore chiaramente provocatorio!), ma la Matematica ci appartiene; è una delle nostre usuali facoltà mentali così come lo è la capacità di esprimerci attraverso il linguaggio. [1]
Se queste argomentazioni ci giungono da parte di ricercatori tutti occupati dal risvolto strettamente connesso alla scienza matematica, è interessante completare, in questa sede didattica scolare di scienze, anche il risvolto che riguarda la ricerca della scienza biogenetica, poiché è stato continuamente tirato in ballo il gene della matematica fra i diversi altri geni.
I geni architetti, geni preistorici
È interessante il percorso della ricerca scientifica biogenetica – la biologia molecolare in particolare – seguito da un noto ricercato, il prof. Edoardo Boncinelli. Tempo addietro, nel 1998 ha espresso, com'è suo solito in modo davvero pittoresco, le sue concezioni in biogenetica riportate dalla rivista mensile Newton di ottobre. Sintetizzo di seguito l'articolo a riguardo pubblicato su questo periodico.Secondo Boncinelli, la testa dell’uomo, come di qualsiasi vivente, nel cominciare a prefigurarsi alla vita terrena, segue un certo itinerario genetico, in netto anticipo sul resto, pur esso in formazione secondo gli schemi cromosomici.
«I geni che formano la testa cominciano a funzionare quando ancora l’embrione “non sa” dove avrà la testa e dove i piedi. In questa fase, la porzione dell‘embrione che diventerà la testa è smisuratamente grande rispetto al resto, come se la natura si sia voluta concentrare sulla parte più nobile di un individuo, lasciando perdere temporaneamente il resto».
I suddetti geni architetti – prosegue il prof. Boncinelli – «probabilmente rappresentano la nostra parte più antica rimasta sostanzialmente inalterata da quando comparvero sulla terra i primi animali dotati di testa, cioè subito dopo le meduse nella scala evolutiva». Di qui si rivela il lato giocoso e polarizzante di Boncinelli con una conclusione a modo suo congeniale. Egli dice che «la bellezza di questa ricerca è proprio nell‘aver mostrato che il progetto fondamentale del corpo umano è stato deciso centinaia di milioni di anni fa e che tutti gli animali oggi esistenti, uomo compreso, non rappresentano che delle variazioni al tema».
«Un bambino inizia a svilupparsi con l’attivazione di questi geni “preistorici”, quindi, è come se in pochi giorni ripercorresse l’intera storia evolutiva».
In particolare, Boncinelli ed il suo gruppo di ricercatori del Dipartimento di biotecnologie dell’Istituto San Raffaele di Milano, avevano fatto progredire le ricerche sui geni architetti del cervello, scoprendone un altro, chiamato EMX-2.
Il ruolo di EMX-2 nella progettazione e costruzione della corteccia cerebrale venne chiarito dallo stesso gruppo nel 2000 e allora si parlò di EMX-2 come del “gene che regola il pensiero”. Anche adesso l’entusiasmo è grande.
Per Michèle Studer, il processo di suddivisione cerebrale controllato dal gene COUP-TFI potrebbe costituire la base neurologica della famosa “teoria delle intelligenze multiple”, elaborata 25 anni fa da Howard Gardner, professore di psicologia dell’età evolutiva all’Università di Harvard, a partire da osservazioni sullo sviluppo delle capacità cognitive nei bambini. La teoria di Gardner scardinò il tradizionale concetto di intelligenza, intesa come capacità generale, misurabile con il QI, sostenendo che l’intelligenza risulta dalla combinazione di alcune abilità mentali più o meno sviluppate, o meglio, esistono diversi tipi di intelligenza, sette o anche otto o forse più. In realtà la teoria psicologica di Gardner ha rivoluzionato anche il modo di vedere il sistema cervello-mente: non un elaboratore centrale, ma l’insieme di sistemi di elaborazione fondamentali e distinti. La ricerca dei geni - probabilmente più di due, forse una decina - responsabili di questa straordinaria architettura è aperta.
Per chi volesse approfondire la cognizione sulla ricerca del prof. Boncinelli, rimando ad un pdf presente sul sito dell'università di Udine (consulta il link alla fine del post).
Geni architetti “dilettanti”- L'opinione di un dilettante
Nello studio della matematica, c’è opinione degli stessi accademici che, per prima cosa, molte creazioni matematiche sono storicamente state fatte da cosiddetti “dilettanti” (che è poi solo un modo di dire: a volte la loro cultura è tutt’oggi invidiabile da parte di tanti “accademici”). Per seconda cosa, quel che conta nella ricerca matematica è spesso lo spirito creativo, l’idea geniale, la curiosità, doti che non sempre richiedono una grande cultura matematica.
Ma le creazioni riguardano anche innumerevoli altre discipline della scienza e perciò anche in tutti questi ambiti si annoverano altrettante creazioni attribuite ai “dilettanti” in questione.
Ne abbiamo una prova proprio nel contesto di questo scritto, con il prof. Boncinelli, fisico di formazione, ma biologo molecolare di mestiere, oggi anche filosofo.
Chi abbiamo di fronte? Per certi versi, senza per questo sminuire il suo indubbio prestigio accademico, potremo accettare l'idea che la sua carriera di ricercatore insigne è cominciata in modo “dilettantististico” partendo, però, da una posizione di tutto riguardo, la laurea in fisica.
Boncinelli ha dunque cominciato a “nascere” come studioso “autodidatta” delle scienze della vita, ed è diventato poi pioniere delle discipline scientifiche che attualmente hanno raggiunto i massimi livelli di specializzazione. Discipline che alla fine degli anni ’60 cominciavano a muovere i loro primi passi.
Ma, per certi altri versi, è così anche per il prof. Butterwort, professore di neuropsicologia cognitiva, col suo libro “Intelligenza matematica”, per esempio. Ha affrontato un considerevole lavoro addentrandosi nel mondo dei numeri, eppure egli sin dall'inizio della stesura del suddetto libro ci tiene a dire: «Io non sono un matematico. In effetti, non sono particolarmente bravo né in matematica né a far calcoli.»
Un altro esempio, che sembra avere le connotazioni risalenti a geni del genere “dilettante”, è il caso di Hunting del film «Will Hunting, genio ribelle», del quale ne parlo nel post «Competenti e incompetenti con i numeri» di Matem@ticaMente.
Egli è un giovanotto che lavora come inserviente al MIT, la più prestigiosa Università scientifìca del mondo. Si tratta però di un film, ma la sua trama è interessantissima, non solo sotto il profilo umano, ma anche per il lato scientifico che con questo scritto si sta affrontanto, senza alcuna pretesa accademica naturalmente. È una mia semplice opinione di meno che dilettante in materia.
E così, seguendo la trama del film in discussione, si viene scoprire che Will Hunting risulta essere un prodigio in matematica alla stregua di Ramanuhjan, il più grande di tutti.
Il professore che poi si occupa con amore di lui, pur essendo insignito di una medaglia Fields – una specie di premio Nobel per la matematica, solo che viene assegnata ogni quattro anni – ne è affascinato. «Non sono niente in confronto a questo ragazzo», ammette.
Gaetano Barbella
- Scarica il pdf sulla ricerca del prof. Boncinelli: "L'origine della forma vivente"
_________________________________
POST CORRELATI
- Intelligenza Matematica
- Tabelline e Matematica
- Competenti E Incompetenti Con I Numeri
giovedì 13 marzo 2008
Scoprire Le Sostanze Chimiche Nel Quotidiano
Cari colleghi,metto a disposizione, di quanti fossero interessati, il pdf dell'unità di apprendimento "Scoprire le sostanze chimiche nel quotidiano", da me redatta per la rivista Scuola e Didattica, Editrice La Scuola - Brescia (nel piano delle pubblicazioni relative all'annata 2007/08).
L' unità di apprendimento si trova sul numero 12 della citata rivista, uscito il primo Marzo 2008, alle pagine 31-32-33-34, Sezione "Scuola in atto", classi 1°.
Troverete il link per scaricarla alla fine del post.
Riporto di seguito l'introduzione alle "Attività laboratoriali". Il resto potrete consultarlo dopo aver scaricato il pdf dell'articolo.
*****
Il percorso di apprendimento sulle sostanze chimiche può essere avviato in vari modi poiché l’argomento si presta a molteplici spunti. Ad esempio, si potrebbe optare per la lettura di un passo tratto da Il sistema periodico di Primo Levi, in cui il protagonista, divenuto poi un chimico, descrive alcuni affascinanti esperimenti di laboratorio vissuti in modo clandestino all’età si 16 anni.
“ Era gennaio. Enrico mi venne a chiamare subito dopo pranzo: suo fratello era andato in montagna e gli aveva lasciato la chiave del laboratorio. Mi vestii in un attimo e lo raggiunsi in strada (…).
Il laboratorio era rudimentale (…). C’era un bancone piastrellato, poca vetreria, una ventina di bocce con reattivi, molta polvere, molte ragnatele, poca luce e un gran freddo. Lungo tutta la strada avevamo discusso su quello che avremmo fatto, ora che saremmo << entrati in laboratorio >>, ma avevamo idee confuse (…)”.
Il laboratorio era rudimentale (…). C’era un bancone piastrellato, poca vetreria, una ventina di bocce con reattivi, molta polvere, molte ragnatele, poca luce e un gran freddo. Lungo tutta la strada avevamo discusso su quello che avremmo fatto, ora che saremmo << entrati in laboratorio >>, ma avevamo idee confuse (…)”.
In prima, la dimensione fantastica in un percorso apprenditivo è molto importante per favorire la motivazione nei riguardi di un argomento non certamente facile e tenere alta la tensione cognitiva. Tali considerazioni non escludono di optare per un taglio problematico, che mira a stimolare sia la formulazione di ipotesi attorno ad alcune domande che le successive proposte di soluzione.
Il percorso illustrato di seguito, si ispira, come vedremo, all’impostazione appena indicata. Resta inteso che questo è soltanto un primo approccio allo studio della chimica, che sarà affrontata ciclicamente negli anni successivi di studio, aggiungendo progressivamente un nuovo tassello alla sua comprensione. In prima, data l’età dei ragazzi, ci si baserà sullo studio dell’aspetto macroscopico legato alla trasformazione delle sostanze chimiche, rimandando in seguito gli aspetti formali.
*****
Scarica qui il pdf dell'unità di apprendimento.
________________________
lunedì 10 marzo 2008
Esplora Una Tavola Periodica Degli Elementi Dinamica: Ptable
Cari lettori, segnalo, in questo post, Ptable, un tool (strumento) dinamico di indiscussa valenza didattica.
Ptable è, infatti, una tavola periodica degli elementi chimici veramente interessante, che consente di esplorarne agevolmente le diverse caratteristiche: proprietà, orbitali, massa, nomi, configurazioni elettroniche e altro.
Una sua utile peculiarità è quella di consultare wikipedia, cliccando su ogni singolo elemento della tavola. Disponibile anche una versione statica rimpicciolita in formato PNG, consultabile online. E’ possibile, inoltre, richiedere, dietro pagamento, un poster personalizzabile.
Tra le numerose lingue disponibili, è incluso anche l’italiano.Cosa volete di più? Non vi resta che consultarla per scoprirne le potenzialità.
Vai a Ptable.
domenica 9 marzo 2008
La Teoria Delle Stringhe
Secondo questa teoria, studiata da molti scienziati, le fondamentali forze della natura e le particelle elementari, costituenti la materia, sono in realtà minuscole cordicine vibranti.
In questa visione, l'Universo non è altro che una grande sinfonia e le varie particelle (quark, fotoni, elettroni ...) sono le diverse note che la compongono!
Teoria originale e suggestiva, una teoria del Tutto, che tenta di descrivere la realtà nel suo complesso: dalle particelle elementari all'Universo.
Un obiettivo ambizioso in vista del quale si stanno percorrendo diverse strade.
Cliccando sull'immagine, raggiungerete la pagina di Focus.it, dove potrete guardare l'interessante filmato in Flash.
_________________________
POST CORRELATI
- La Nebulosa Rosetta Per Il Valentine's Day
- L'Universo Visto Da Un'Astronave
- Conspiracy Of Science - Earth Is In Fact Growing
giovedì 6 marzo 2008
Mappe Concettuali: Un Percorso Di Ricerca Sull'Acqua
presento, in questo articolo, un percorso di ricerca didattico - metodologica sulle mappe concettuali, svolto all’interno del mio Istituto Comprensivo, già presentato da Maestro Alberto (che ringrazio di cuore) qualche mese fa. Lo metto a disposizione anche su questo blog.
Il percorso, che ha coinvolto tutti e tre i gradi scolastici (scuola dell’infanzia, scuola primaria e scuola secondaria) sulla tematica “Acqua“, ha portato alla realizzazione di diversi materiali per i tre ordini scolastici.
Per la scuola dell’infanzia:
• un’ampia documentazione di un percorso didattico, centrato sulla tematica “Acqua”, realizzata attraverso le mappe concettuali (7 mappe) dall’individuazione dei contenuti didattici, distillati ad hoc per il livello scolare 5/6 anni, all’enucleazione degli elementi della valutazione e di quelli metodologici, compresi gli obiettivi formativi da perseguire.
Per il primo biennio della scuola elementare:
• una mappa concettuale sulla tematica “Acqua”, corredata di tre esperimenti, esemplificativi di uno dei possibili percorsi da attuare, e da una valutazione dell’attività proposta. inoltre dei cloze e altre mappe.
Per la scuola secondaria:
• un decalogo di istruzioni su come realizzare una mappa concettuale;
• una mappa rappresentante le “tre forme dell’apprendimento cognitivo in interazione fra di loro”;
• una mappa relativa alle “due forme di acquisizione dei concetti e le loro relazioni con l’esperienza e la struttura cognitiva”;
• 4 mappe, realizzate su tematiche diverse allo scopo di documentare l’inesauribile flessibilità del loro impiego.
I materiali contengono, inoltre, varie mappe prodotte dagli alunni e ulteriori risorse. Il percorso può essere generalizzato dai docenti, che volessero utilizzarlo, alle proprie situazioni didattiche, naturalmente adattandolo con la flessibilità richiesta.
Scarica i materiali:
- percorso di ricerca-azione (documento .pdf)
- acqua scuola secondaria 1° grado
sabato 1 marzo 2008
Riflesso In Autunno: Maroon Belles (Colorado)
Cari ragazzi, continua il reportage fotografico dall'America con un'altra splendida fotografia panoramica del nostro amico Gale Rainwater.
Questa volta è una vista delle Maroon Belles, nelle Montagne Rocciose del Colorado, ancora sul tema dei colori d'autunno.
_______________________________________
POST CORRELATI
- Colorful Colorado: I Colori Autunnali
- I colori dell'Autunno allo Yellowstone National Park
- Reportage fotografico con flickr
Questa volta è una vista delle Maroon Belles, nelle Montagne Rocciose del Colorado, ancora sul tema dei colori d'autunno.
_______________________________________
POST CORRELATI
- Colorful Colorado: I Colori Autunnali
- I colori dell'Autunno allo Yellowstone National Park
- Reportage fotografico con flickr